Some argue that the tournament is already too large, because its size "devalues" the regular season just as the NBA playoff format makes its regular season nearly meaningless. That's a little extreme, but increasing the tournament size might make the analogy exact.
If we begin with the notion that the tournament should include the top n teams then the first question is "what should n be?"
Actually, it's a little trickier than that, because we have to include conference champions outside of the top n, and logistically the tournament has to have size equal to an even multiple of four.
So we want tournament size m such that m ≥ n+k and m = 8×j where k = the number of conference champions outside of the top n and j is any integer that satisfies the relation. For aesthetic reasons (and some practical ones to be discussed below) we prefer the smallest such j.
The requirement that m be an even multiple of four is "weak" if we allow the concept of "play in games." Any tournament size m = 8×j where j is not a power of 2 requires a first "round" that doesn't include all of the tournament teams. Having one (as we do now), two, three, or however many such games to reduce the field to a size that is an exact power of two is reasonable. So if we wish, we may take m = 8×j + l (for l ≤ 7) just as the current format has 65 = 8×8 + 1.
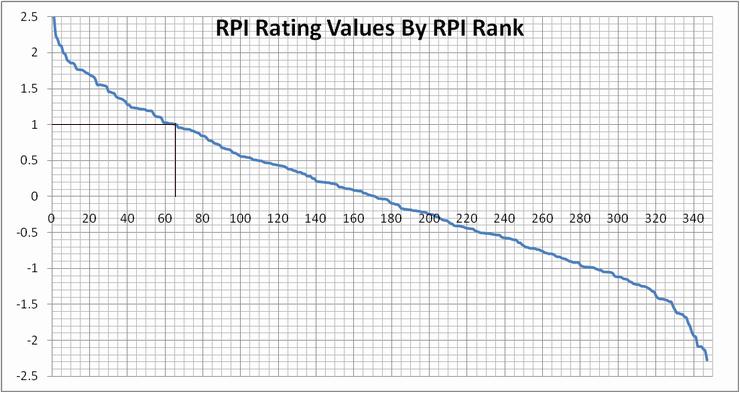
I say "any objective measure" because it is reasonable to expect that team quality ("top-ness") conforms to a normal ("bell curve") distribution, and so do all of the objective measures we might choose. (Actually, a measurement that does not have values that are normally distributed is probably a bad choice.)

|
I chose the ½ standard deviation increments as a convenient way to assign a "grade on the curve" to each team: teams with ratings greater than two standard deviations above the average get an A+, teams with values greater than 1.5 standard deviations above average but less than or equal to 2 standard deviations above average get an A, and so on with different grades for each ½SD increment.
When "grading on the curve" a "C" is assigned to all values within ± 1 standard deviation of average.
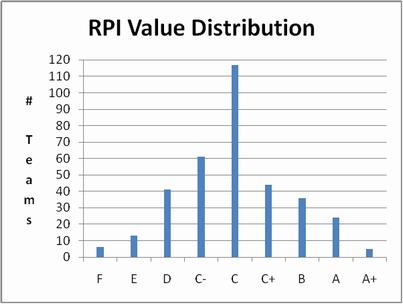
If we define the very top ½ standard deviation of that range as "C+" and the bottom ½ as "C−" we find the distribution of RPI values looks like the one to the left.
That the total number of teams in grades B or higher is 65 isn't a coincidence - that's the way the mathematics of normal distributions works. That the NCAA tournament is the same size probably is. But the tournament doesn't include all of the teams with a B or better grade, because it includes the automatic qualifiers from conferences with no such teams. |
|
To check the impact of automatic qualification, just count the number of teams with each grade for each conference. (Here I divided "C" into "C higher than average" - C> and "C lower than average" - C<.)
There are 16 conferences with automatic bids that don't have any teams with a grade B or higher. (Independents can only receive at-large bids and the Great West doesn't yet qualify.) So if the goal is to have the "best 64" teams in the tournament, we fall 16 short of that.
But there are good reasons to believe that's not the right objective. Even with "only" 20 spots available for the 36 "B" (for "bubble?") teams, there are some who argue that some of those 20 aren't "tournament worthy."
In fact, I began this analysis when I read an opionion that the tournament was already too large! There are other criteria than how well a team's season is graded by any particular measurement.
As good as computer ratings are for measuring the entire season, they don't take into account things like injured players, give extra credit (explicitly, anyway) for record vs other contenders, and so forth. The committee decides which of the B (or worse) -teams to include. It's the committee's job to pick which 20 or so teams out of 36 or so candidates.
Above I said we want j to be as small as possible. The reason is that the farther you go into the "middle of the pack" there are more teams that are equally good mediocre. With the current 64/65-team tournament, all of the "B"ubble teams are at least good choices for the committee.
The big loser in a large expansion would be the committee. If today they have to hold their nose while selecting the 20th team of 36 candidates, having to even look at the 46 teams whose resumes are worse than the current worst bubble team's might cause serious injury.
If there's a problem with current tournament size (and it is not obvious that there is) it is that because of the automatic bids for really bad conferences some teams arguably as good as the last teams in are left out.
That's not going to be fixed by eliminating automatic bids, so increasing the tournament size is the only alternative. But a leap to a 96-team tournament has more downside than up.
If the price of the "fix" is diluting the quality of tournament teams, the right way to do that is increase the number of play-in games. That will allow more bubble teams to be included without expanding the size of the bubble.
My personal opinion is that not only is there no good reason to expand the tournament to 96 teams, there's not even a bad reason to. Just check the TV ratings for the play-in game to price the ads for a first round involving seeds 33-96.